Derivatives 101: 9

Despite a brief allusion in the previous installment to the stochastic nature of pig prices, there has so far been no attempt to explain what that actually means; and, to be frank, that's not about to change. Such an attempt would be tedious and difficult and this is, after all, first and foremost a frivolous exercise.

That said, there are some characteristics of stochastic processes that are interesting in their own right, and they are relevant to the matter of derivatives pricing, with which we are at least pretending here to be vaguely concerned, so let's allude a little further and see where it takes us.

Although there is some distinction in the way the terms are used, stochastic is just a synonym for random. If something behaves randomly, it is said to follow a stochastic process¹. Stochastic processes are discontinuous and unpredictable: at a given moment it is impossible to say with any certainty what their value will be a moment later². The best you can do is offer a probabilistic assessment: there is an x% likelihood that it will be between A and B. You can lay odds. Make book.

Randomness is an intuitively simple idea, but it turns out to be remarkably difficult to pin down. People are famously bad at understanding things like probability and risk, which is why gambling is such a profitable business; but it wouldn't be if there weren't tools for dealing with this stuff beyond the flawed visceral human response. If bookies were as clueless as their punters they wouldn't be in business for long.

One of the key ways in which random processes can be understood is in terms of their distribution; distributions are the geography of randomness.

For instance, let's say we roll an ordinary, fair, six-sided die. The "fair" bit means the result is totally random, equally likely to be any of the numbers from 1 to 6. This is called a uniform distribution: easy peasy, right?

Do that twice, and add up the results of both rolls. Is the sum uniformly distributed? The answer, as you probably know, is no; and the reason is that there is a structural relationship between the total and the two separate uniformly distributed rolls: there's only one way they can add up to 2 or 12, whereas there are 6 ways they can add up to 7. The more times you roll, the more detailed the relationship becomes, and as the number of rolls tends to infinity the distribution of the results tends towards the single most important distribution in the realms of probability and statistics, called the Gaussian or normal distribution: the notorious bell curve³.

Stochastic processes come in a range of shapes and sizes, but the ones we would be interested in, were we to be interested, which I have to emphasize we aren't, are Markov processes; which is to say, they have no memory. In particular, Wiener processes (aka Brownian motion) and Itô processes. The gory details need not concern us; suffice to say that the former is your basic source of normally-distributed randomness, while the latter is an elaboration that takes that basic randomness and varies it over time in more or less interesting ways.

This relationship between underlying randomness and more complicatedly unpredictable behaviour might seem cognate with our discussions of traded derivative instruments, and as it happens that resemblance is both meaningful and productive, but let's not jump the gun.

A key result in dealing with stochastic processes is Itô's Lemma, which has a precise mathematical formulation in symbols that I really can't face trying to express here, but which in essence asserts a transitivity relation: if A follows an Itô process, and B is a function of A (and time), then B also follows an Itô process. The two share the same underlying source of uncertainty and there is a well-defined⁴ way of getting from one to the other.

You may by now be wondering what the hell any of this has to do with the price of pigs.

Well.

It is common -- which is not to say necessarily correct, we're just trying to scrape a living here -- to model the price fluctuations of a stock⁵ as a Generalized Wiener process, which is a particular (and relatively simple) case of an Itô process, driven by Brownian motion⁶.

From one point of view, this merely restates our proposition from yonks ago that the future is unknowable -- duh! -- but with a rider that we might be able to make educated guesses about some future things with some degree of confidence. In particular, we might be able to say something about how, taken en masse, the behaviour of a large number of stocks over a large amount of time might be distributed.

Now, consider a derivative instrument D whose value V_d depends on some underlying stock S, currently priced at V_s. The details of that dependency will vary from derivative to derivative, but that is by the by; the important thing is that at any given time t the relationship will be quite concrete, laid down by D's contractual terms.

V_d, that is to say, is a function of V_s and t.

If we are modelling V_s as an Itô process, then by Itô's Lemma, V_d must also follow an Itô process, with the same fundamental source of randomness. Consequently, over any very short period of time Δt there will be a pretty direct relationship between the two values: V_d is, instantaneously, some multiple of the value of V_s.

What this means -- and this is where you line up for your Nobel Prize, kiddo -- is that it is possible⁷ to construct a porfolio of S and D that is risk free: any (short-term, random) change in the value of the stock (S) is exactly counterbalanced by a proportionate change in the value of the derivative (D).

We already know that we can invest money at some risk-free rate, and we know that the value of any investment is, in some impossible-to-pin-down way, proportional to its risk. The only case where we can ground this with any certainty is when that risk is zero.

A riskless investment is a riskless investment. It doesn't matter what it is, the payoff must be the same -- otherwise arbitrage is possible and that only leads to tears. If our portfolio of D and S is riskless, it must by definition earn exactly the risk-free rate; and since the worth of S is a matter of public record, that gives us everything we need to -- instantaneously -- value D.

That, in a misrepresented nutshell, is the Black-Scholes-Merton argument for pricing derivatives, which can be neatly expressed in a partial differential equation that looks like this:

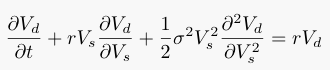
(where V_s is the underlying price, t is time, V_d is the derivative price, r is the risk-free rate and σ is the volatility of V_s -- which is to say, its standard deviation, a measure of how wildly it fluctuates).

One of its interesting consequences is to retroactively define what constitutes a derivative: any instrument that doesn't satisfy the equation is, at least in theory, open to abuse by arbitrageurs, and thus not a sustainable derivative at all.

Even though all this is rather abstract and theoretical, it is effectively holy writ to the people⁸ who run the financial world and is (with certain caveats that we may or may not address in the next and final episode) consequently the way things really work.

Re-read it, my bewildered children, and weep.

---

[1] The implication is that the "process" is the source of the randomness, while the observable behaviour is just a symptom of it. If this notion seems at all familiar, award yourself a gold star.
[2] Here, "moment" stands for whatever length of time you feel like.
[3] The reason the normal distribution is so important is not that lots of things are normally distributed, although they are, but that the sum of samples from any distribution tend to it. This is called the Central Limit Theorem, and it is one of the foundations of statistics. Whenever you see a confidence interval ("the chances of this genetic fingerprint being wrong are 1 in 10,000,000,000") or a tolerance ("86% of gay men who've seen Superman Returns think Brandon Routh is gorgeous (±2%)") in the press, you can be pretty sure the Central Limit Theorem is involved.
[4] The definition involves partial derivatives -- that's calculus derivatives, not the financial instrument kind -- so it depends on B's differentiability, but let's not concern ourselves with such sordid details.
[5] By "stock" I of course mean shares in a company rather than livestock. Equities and commodities are not at all the same thing, but fuck it, it's more fun to talk about pigs than shares in Microsoft.
[6] Brownian motion was originally observed with grains of pollen suspended in a fluid. The mathematical equivalent attempts to model the net effect of lots of tiny fluid molecules randomly battering against a pollen grain some orders of magnitude larger. In the context of finance, we can imagine a stock price being buffeted by the purchasing decisions of a multitude of tiny investors. Of course, the investment landscape isn't as homogenous as molecules in a simple fluid -- it has more the chunky constituency of fresh vomit -- but let's assume that a larger investor will be proportionally more diversified and it all evens out. (This is one of those assumptions I referred to way back that are self-evidently wrong but nevertheless useful.)
[7] Given a lot of assumptions, the most crucial of which is that short positions are allowed; that is to say, you can hold a negative amount of an asset. There is a mechanic by which this makes sense, but be warned: thinking about it too hard will permanently damage your brain.
[8] In the loosest possible sense of the word.
Posted by matt at July 28, 2006 12:02 AM