The End

Mainly: not to do it again. I mean, it was fun at first, but when you make something a duty it soon starts to feel like a chore. More than a few of these entries have been dreary to write and even drearier to read, and really, who benefits from that?

Time, then, to ring down the curtain. On this unwieldy month and also, I think, on WT as we know it. Five years in one incarnation is enough. It has been, as always, a slice, but now let's call it done and see what comes next.

Au revoir, mes enfants.

Lies, Damned Lies and WT

Well, a little Perl hackery provides some summary stats: there've been 772 posts on WT (including When@, but not including this one), with a total body text length a bit shy of 300,000 words; the word counting is pretty crude, though, so take this with a pinch of salt. Average post length was 375 words, with the shortest entry a mere two words and the longest 3,830. Average number of comments on a post was 2.6, with an obvious minimum of zero in too many cases to mention, maxing out at 47 on one memorable occasion. That was long ago, of course. I fear we peaked early.

Some further mucking around in R reveals slightly more, or perhaps it doesn't. The progress of post lengths and comments over time is pretty unilluminating: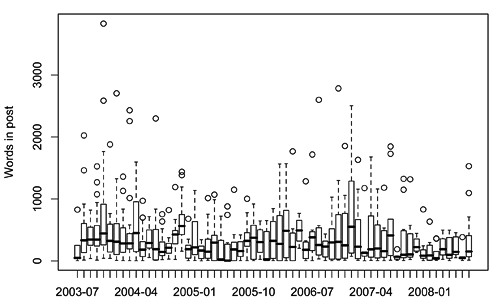

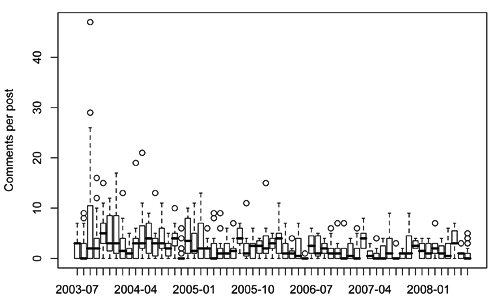When you consider just the overall distributions, though, they seem to be roughly exponential (or I guess more properly geometric, since both are discrete quantities):

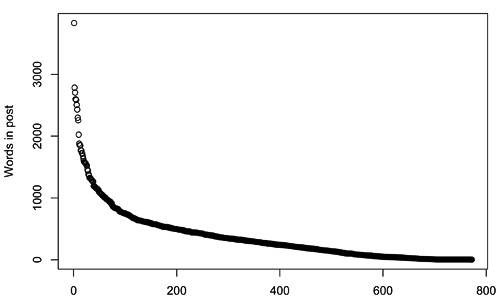
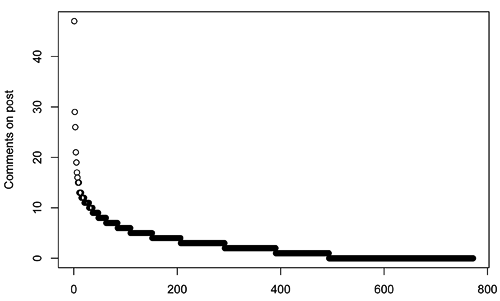Is this surprising? Probably not. This is the sort of distribution that governs things like how long you'll wait for a bus -- and, for that matter, the opening of ion channels. It's pretty much what one would expect if you and I were both posting completely at random...

Finally, here's a sorry but rather familiar tale:

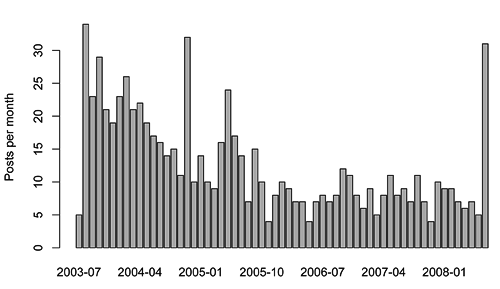There are a few odd spikes -- Incognito, for instance, and indeed the current not-quite-over month -- but the trend downwards to a rather low baseline is clear enough.

On the other hand, at least I've asymptoted to something above zero. Unlike certain others I could mention...

Boys, Toys, Electric Irons and TVs

Fast

There's little chance of me wasting away, what with my reserve stores and all, but I am beginning to get mightily pissed off...

Disappointments

Notably, The Dark Knight seemed distinctly under par, noisy and disjointed and much less interesting than it ought to have been, despite an entertaining if mannered turn from Heath Ledger. There were certainly some diverting moments, but it failed to hang together in a very disappointing way.

Also falling rather short of expectations was the Hayward's Psycho Buildings exhibit, a not terribly successful attempt to present the engagement of artists with the business of architecture. One or two of these collisions were sort of interesting, but the whole collection seemed rather gimmicky and pointless. I enjoyed rowing on the flooded sculpture terrace, but it really wasn't nearly as interesting an engagement with space as the children's favourite out front of the QEH, Appearing Rooms.

Ho, essentially, hum.

The Q Continuum

The thing is, I am almost entirely persuaded that the techniques under discussion represent the right -- which is to say, the best available and most theoretically correct -- way to go about things. I can also see why so few people do. It's not because the whole thing is conceptually difficult -- bits of it certainly are, but not outlandishly so in the already-abstruse context of electrophysiology. But it simply isn't available in a form that is accessible to someone not already institutionalised by years of exposure to the software quirks, even if that someone is otherwise well-versed in the intricacies of single channel recording.

At one level, I'd really like to do something to improve this particular situation, but it's not clear what that might be. The obvious approaches represent a huge amount of work, and would be to the benefit of almost no-one; they are, in consequence, not all that appealing. But I'll be looking into it in the coming weeks, so maybe there'll be some worthwhile contribution I can make.

I have, you may note, completely glossed over the actual meat of the subject, and I don't propose to attempt any kind of explanation here; at least, not just now. But, purely as a token, here's the "mug" equation, which gives the expected burst length distribution for an ion channel whose behaviour is characterised by a mechanism Q, assuming the recording apparatus is perfect, which it never is:

f_b(t) = φ_b [e^Q_EEt]_AA (G_ABG_BC + G_AC) u_C

And here's some Matlab code to calculate this, along with the corresponding open and shut time distributions, under the same unrealistic measurement conditions.

function [A lambda] = spec ( M )
% SPEC generates the spectral expansion matrices of the supplied matrix
% [A lambda] = SPEC(MATRIX)
% A is a cell array of the spectral expansion matrices
% lambda is a vector of the corresponding eigenvalues
[h v] = size(M);
if ( h ~= v ), error 'supplied matrix must be square!'; end

A = {};
[V, D] = eig(M);
rV = inv(V);
lambda = diag(D);

for k = 1:h
    cE = V(:, k);
    rE = rV(k, :);
    A{k} = cE * rE;
end;


function B = sylv ( M, f, args )
% SYLV calculates a function of a matrix using Sylvester's Theorem
% B = SYLV(MATRIX, FUNC, ARGS)
% FUNC must be of the form RESULT = F(MATRIX, ARG)
% B is a cell array containing the results for all ARG in ARGS
[h v] = size(M);
if ( h ~= v ), error 'supplied matrix must be square!'; end

[A lam] = spec(M);
B = {};

for r = 1:length(args)
    Br = f(lam(1), args(r)) * A{1};
    for k = 2:h
        Br = Br + f(lam(k), args(r)) * A{k};
    end
    B{r} = Br;
end


function [D_o D_s D_b] = qideal ( Q, kA, kB, kC, t )
% QIDEAL calculates the ideal open, shut and burst time distributions for a Q matrix
% [f_open f_shut f_burst] = QIDEAL( Q, kA, kB, kC, t )
%
% Q must be in canonical form, with A (open) states before B (fast shut) before C (slow shut)
% kA, kB and kC are the number of each kind of state
% t is a vector of time points for which to calculate the f values
%
% no account is taken of the distortion caused by missed events, and error checking is minimal
[h v] = size(Q);
if ( h ~= v ), error 'Q matrix must be square'; end

kF = kB + kC;
kE = kA + kB;
k = kA + kF;

if ( k ~= h ), error 'kA + kB + kC is not the same as k'; end

% get the partition matrices
Q_AA = Q(1:kA, 1:kA);
Q_AF = Q(1:kA, (kA+1):k);
Q_FA = Q((kA+1):k, 1:kA);
Q_FF = Q((kA+1):k, (kA+1):k);

Q_BB = Q((kA+1):(kA+kB), (kA+1):(kA+kB));
Q_CB = Q((kE+1):k, (kA+1):kE);
Q_CA = Q((kE+1):k, 1:kA);
Q_BA = Q((kA+1):kE, 1:kA);
Q_AB = Q(1:kA, (kA+1):kE);
Q_EE = Q(1:kE, 1:kE);

% define the (time independent) G matrices
G_AF = inv(-Q_AA) * Q_AF;
G_AB = inv(-Q_AA) * Q_AB;
G_BA = inv(-Q_BB) * Q_BA;

% calculate equilibrium occupancies
S = [Q, ones(k,1)];
p_inf = ones(1,k) * inv(S * S');

% calculate initial state vectors
pF_inf = p_inf((kA+1):k);
phi_o = pF_inf * Q_FA;
phi_o = phi_o / sum(phi_o);

phi_s = phi_o * G_AF;

pC_inf = p_inf((kE+1):k);
phi_b = pC_inf * (Q_CB * G_BA + Q_CA);
phi_b = phi_b / sum(phi_b);

% calculate burst-end vector
e_b = (eye(kA) - G_AB * G_BA) * ones(kA, 1);

% f_open(t) = sum(phi_o * exp(Q_AA * t) * Q_AF)
% f_shut(t) = sum(phi_s * exp(Q_FF * t) * Q_FA)
% f_b(t) = phi_b * exp(Q_EE * t)_AA * (-Q_AA) * e_b
f = @(x,t) exp(x*t);
expQA = sylv(Q_AA, f, t);
expQF = sylv(Q_FF, f, t);
expQE = sylv(Q_EE, f, t);

D_o = zeros(size(t));
D_s = zeros(size(t));
D_b = zeros(size(t));

for ti = 1:length(t)
    D_o(ti) = sum(phi_o * expQA{ti} * Q_AF);
    D_s(ti) = sum(phi_s * expQF{ti} * Q_FA);
    
    tmp = expQE{ti};
    D_b(ti) = phi_b * tmp(1:kA,1:kA) * (-Q_AA) * e_b;
end

Generating realistic distributions is a much more difficult problem. If I manage to get to grips with the key 1990 and 1992 papers by Hawkes, Jalali & Colquhoun I may post code for that too. I want it clear from the start, however, that I will not attempt any kind of fitting. That stuff has an SEP field the size of Kazakhstan around it...

Unfortunate

"You're upset about being embarrassed?"

"Yes "

...

A Holiday From Death

The Cholmondeleys and Featherstonehaughs's latest is, frankly, barely a dance piece at all. It's an end-of-the-pier exercise in fatalism, a hysterical post-mortem high-kick in the teeth to the platitudinous posturing of religious reassurance, urging:

Framed as an old time music hall act with greasepainted banjo players and a pantomime chorus, Dancing On Your Grave manages to be formally unchallenging whilst really rubbing one's nose in it. The bare facts of our existence are relayed in a beautifully simple, brutal, humane -- and utterly entertaining -- fashion. It's great.

Go see.

Coincidence?

My memory of much of this is still surprisingly clear, given that I last heard any of it in something like 1982. Cal it a consequence of having listened to my off-the-air tapes countless times back then: this stuff is engraved on my brain in a way that I just can't seem to manage now with any number of much more useful things. Despite that, I turned out to be slightly vague on the details of dessert -- I thought the ice cream flavour was vanilla, for example -- and so it seemed worth a google.

Make no mistake, I've done that before -- at the time of those earlier posts, for sure, and at other times as well. I don't remember when the last attempt was, but at that time Hordes of the Things was still effctively unknown to the internet, and thus could only tentatively be said to have existed at all. Given the inexhaustible depths of trivia long since available online, I was beginning to wonder whether I'd imagined the whole thing. Perhaps it was some kind of ludicrous adolescent fantasy that just didn't hold up to adult inspection.

Well, no. My ancient recollections have been unexpectedly vindicated.

That there might now be a Wikipedia entry for this long-forgotten series is not the world's biggest surprise, given that it is increasingly difficult to find any fucking thing for which there is not a Wikipedia entry. What is surprising, though -- almost alarming, in fact -- is that said entry reveals said show to have started repeats on BBC7 just the other day. Indeed, at least for those in the UK, the first episode -- from which most, if not all, of the examples so far cited on WT derive -- is available on iPlayer for the rest of this week.

I mean, really. What are the chances? Is the entire world enslaved to my whims? And if so, does that make me responsible for all the fucking awful, dismally depressing shit going down?

Man, I hope not.

Anyway, this "coincidence" allowed me to correct the ice cream flavour to strawberry. And when I once again have net access I will attempt to record the relevant sequence with Audio Hijack or some equivalent, so if you can't access the legit version I may be able to help.

The reason I can't do the recording right now is that I'm writing underground, in the arches of the Shunt Lounge, a members-ish art bar buried under London Bridge station in a space previously used for such performances as Tropicana and Amato Saltone. Some areas have changed significantly since then, others not. Either way, it's an amazing venue, the sort of place that makes me feel privileged to live here in London in these interesting times. Even despite so much in the world being desperate, agonising shit, local existence is still a fucking miracle. There are doubtless luckier people than me right now, but not many.

Of course, there is a downside, which in this case is that I most likely will not be able to see the performance for which I've come all this way. Apparently all the, rather limited, seats for Dancing On Your Grave have been preallocated -- no doubt to miscellaneous friends and family of the company -- and we mere plebs will have to take our chances. Normally this would piss me off no fucking end, but on account of the great pleasure she's given me over the years I'm prepared to cut Lea quite a lot of slack. In addition to which, the whole Shunt Lounge experience is really quite entertaining. As a nearby milk float puts it:

Isn't there always? And isn't that how things should be?

Menu

Eigenvectors

Admittedly, such distinctions are roughly in the same league as arguments about angels on the head of pin, and I'm happy to respect the preferences of anyone who actually gives a flying fuck one way or the other. Still, at least for someone with a more traditional programming background, there seems to be a measurable loss of marginal utility that comes with all attempts to make programs that do maths look in some way similar to how maths looks when done by human mathematicians on paper -- especially when this involves combining free-form positioning on the virtual page with clunky procedural rules about how the logic flows topographically. I'm not clear whether MathCad provides any of the sensible programming constructs that would make it properly useful -- probably it does -- but I'm damn sure I don't care enough to find out.

In any case, the major intellectual engagement of the day revolved around the spectral expansion of singular matrices. Wait, where are you going? Hello?

A central component of the course, and of ion channel analysis in general, is the so-called Q matrix, which -- in my currently rather vague understanding -- seems to be a transition matrix encoding the probabilities that an ion channel -- or, really, any system following a Markov process -- will shift from one of its possible states to another. Since the system has to be in some possible state, the matrix columns cannot be linearly independent. Therefore, the matrix must be singular, and thus have at least one zero eigenvalue.

Okay, I appreciate that this is probably coming across as total gibberish even to the more sciencey among you. At some level there may be no getting around that, but at least let me try to explain.

A matrix is just a table or array of numbers. That much is pretty easy to understand. Why such things are useful -- and, even more so, the strange interactions between them -- is a bit more problematic. The simplest way I can come up with of describing these benefits is in terms of graphics -- by which I mean the sort of stuff you're looking at on your computer monitor right now, though it would apply even more if you were playing a game on a Wii or PS3.

Everything you look at on a screen occupies a visual space that can be quantified in some number of dimensions. Some of these dimensions -- left or right, up or down, in or out -- are explicitly positional. Others -- say, brightness and colour -- are not. There are perspectives from which such a distinction is artificial, but for now we can just dismiss them. Let's think simply in terms of position.

Thanks ostensibly to Descartes, we know that we can define positions using a small number of orthogonal coordinates. In almost all cases, our basic positional concern for screen viewing is two-dimensional, usually in a plane roughly perpendicular to our viewing direction. Indeed, even when this isn't the case, our brains are pretty good at pretending it is, which is why it's not the end of the world when you go to the movies on a busy night and have to sit right over on the side.

Position, then, is commonly a two-dimensional quantity.

But we know that the two-dimensional context in which we view things is subject to changes in its -- and our -- viewpoint. For example, if we are watching a TV and someone comes along and turns the set upside down, we will see the pictures on the screen as being the wrong way up. The same will be true if the set remains untouched but we decide to stand on our head.

When this sort of thing happens, some kind of transformation occurs, changing our view. At the same time, we normally accept that the change is a matter of perspective rather than anything more fundamental: the TV is still showing the same programme within its own frame of reference. It is our relationship to it that has changed.

That frame of reference change is what is of interest to us right now. It amounts to a transformation of our viewpoint -- and that transformation can often be represented as a matrix. The trick that underlies this is matrix multiplication, which is at first sight a rather abstruse and incomprehensible operation. But all that it really means is that a value in any arbitrary dimension -- say, how far to the left or right an object appears to one's eyes -- depends on some combination of the values it has in all its dimensions -- say, where it actually is in space. This is hardly radical or surprising.

A matrix then, is a way of representing how things in one frame of reference get transformed into another.

This is all fine and dandy until we start to consider frames of reference that have different ranks -- that is, different numbers of dimensions. To pick the most obvious example, there's the three dimensional world on the one hand, and its appearance in a two dimensional image on the other. Under such a transformation, several different things -- a person's shoulder, a tree in the middle distance, a jagged peak on the horizon many miles away -- can all wind up at pretty much the same 2D location -- the same point in the picture. A whole bunch of information about the full three dimensional structure of the scene is necessarily lost when it's converted into a photo in this way.

At some level, this kind of transformation is fundamentally different from one that preserves all its dimensions. The latter is, at least theoretically, invertible -- all of the original scene information can potentially be recovered -- whereas the former is not. Somewhere along the line information is thrown away, such that we can never get it back.

Matrices representing such operations -- where information is not merely transformed but destroyed -- are termed singular. A characteristic of such matrices is that one or more of their eigenvalues is zero.

Eigen-wha-whosits? Well may you ask.

A matrix represents a transformation that can be applied to any vector data of a suitable rank -- eg, a 3x3 matrix can transform positions in any 3d space -- producing a transformed space of rank no greater -- but quite possibly lower -- than the original. In general, the transformation depends not only on the matrix but also on the data. For example, consider the matrix: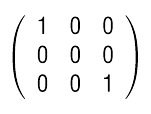

This preserves the x and z dimensions of any data to which it is applied, but any y is brutally truncated to 0. Indubitably, information is tossed away.

Even so, any point -- or vector -- with no y component will slip through entirely unadulterated. Only data in the y direction are lost. Clearly, some information is more liable to be destroyed than other kinds; plenty of information may not be destroyed at all, just perhaps stretched along the way.

We can determine the directions from which data will not deviate under the transform; these are the eigenvectors of the matrix. There are as many of these as the matrix -- which must be square -- has rows or columns. And -- by definition -- every one must be non-zero. Each such vector is associated with an eigenvalue, which is the amount the transformation stretches or shrinks data along that direction. This value can be zero, which was at the root of my confusion today.

A matrix may have one or even more zero eigenvalues, in which case it will be singular. It may not have any zero eigenvectors: even zero eigenvalues must be associated with non-zero eigenvectors.

Because of the way it is formulated, the Q matrix will always have at least one zero eigenvalue. And yet one of the important things we need to do with it -- calculate its exponential -- depends on being able to invert a matrix of its eigenvectors, which in turn requires that that matrix be non-singular. If any eigenvector were zero that would be impossible.

My initial impression was that this would have to be the case, because the Q matrix is singular. No-one present could quite explain why this wasn't so, but fortunately it isn't. Eigenvectors are, by definition, non-zero. When the associated eigenvalues are zero, that just means that there are non-zero vectors that the matrix transforms to zero, and these can be found.

Thus, all remains right with the world. As if you care.

Filler 56

Today was the day of the annual Italian parade and festival in Clerkenwell, of which I've posted photographic evidence in the past. No need to do so again, as it never changes much, but I couldn't in any case as we were absent for the parade itself. Instead, we took young master Oliver, who as you may or may not recall is Ian's godson, to see Wall-E, which I loved to bits. I can't imagine that any of the few people reading this blog need my urging to see it, but if you do, consider yourself urged. It's a marvel.

After that, all that remained was to head back for a glass of prosecco amid the Warner Street throng, an early dinner, and a little preparatory reading for DC's ion channels course, which starts tomorrow and will probably provide some blogging material in the coming days.

Also to come this week, hopefully, are the latest Cholmondeleys and Featherstonehaughs piece at the Shunt Lounge -- period memberships are all sold out, so I'm reduced to queueing on the day -- and, of course, The Dark Knight. That's sold out too for the IMAX (well, there are perfs at 2.30 and 5.30 in the morning, but I'm not that desperate), so I guess it'll have to be boring old Leicester Square...