Eigenvectors

As it turned out, the first day of Understanding ion channels in terms of mechanisms was unexpectedly undemanding. The bulk was spent on matrix algebra, with which I am reasonably familiar, and also the rudiments of MathCad, which turns out to be quirky and irritating in a very similar way to Mathematica, while being apparently less powerful; it's certainly not a patch on Matlab.

Admittedly, such distinctions are roughly in the same league as arguments about angels on the head of pin, and I'm happy to respect the preferences of anyone who actually gives a flying fuck one way or the other. Still, at least for someone with a more traditional programming background, there seems to be a measurable loss of marginal utility that comes with all attempts to make programs that do maths look in some way similar to how maths looks when done by human mathematicians on paper -- especially when this involves combining free-form positioning on the virtual page with clunky procedural rules about how the logic flows topographically. I'm not clear whether MathCad provides any of the sensible programming constructs that would make it properly useful -- probably it does -- but I'm damn sure I don't care enough to find out.

In any case, the major intellectual engagement of the day revolved around the spectral expansion of singular matrices. Wait, where are you going? Hello?

A central component of the course, and of ion channel analysis in general, is the so-called Q matrix, which -- in my currently rather vague understanding -- seems to be a transition matrix encoding the probabilities that an ion channel -- or, really, any system following a Markov process -- will shift from one of its possible states to another. Since the system has to be in some possible state, the matrix columns cannot be linearly independent. Therefore, the matrix must be singular, and thus have at least one zero eigenvalue.

Okay, I appreciate that this is probably coming across as total gibberish even to the more sciencey among you. At some level there may be no getting around that, but at least let me try to explain.

A matrix is just a table or array of numbers. That much is pretty easy to understand. Why such things are useful -- and, even more so, the strange interactions between them -- is a bit more problematic. The simplest way I can come up with of describing these benefits is in terms of graphics -- by which I mean the sort of stuff you're looking at on your computer monitor right now, though it would apply even more if you were playing a game on a Wii or PS3.

Everything you look at on a screen occupies a visual space that can be quantified in some number of dimensions. Some of these dimensions -- left or right, up or down, in or out -- are explicitly positional. Others -- say, brightness and colour -- are not. There are perspectives from which such a distinction is artificial, but for now we can just dismiss them. Let's think simply in terms of position.

Thanks ostensibly to Descartes, we know that we can define positions using a small number of orthogonal coordinates. In almost all cases, our basic positional concern for screen viewing is two-dimensional, usually in a plane roughly perpendicular to our viewing direction. Indeed, even when this isn't the case, our brains are pretty good at pretending it is, which is why it's not the end of the world when you go to the movies on a busy night and have to sit right over on the side.

Position, then, is commonly a two-dimensional quantity.

But we know that the two-dimensional context in which we view things is subject to changes in its -- and our -- viewpoint. For example, if we are watching a TV and someone comes along and turns the set upside down, we will see the pictures on the screen as being the wrong way up. The same will be true if the set remains untouched but we decide to stand on our head.

When this sort of thing happens, some kind of transformation occurs, changing our view. At the same time, we normally accept that the change is a matter of perspective rather than anything more fundamental: the TV is still showing the same programme within its own frame of reference. It is our relationship to it that has changed.

That frame of reference change is what is of interest to us right now. It amounts to a transformation of our viewpoint -- and that transformation can often be represented as a matrix. The trick that underlies this is matrix multiplication, which is at first sight a rather abstruse and incomprehensible operation. But all that it really means is that a value in any arbitrary dimension -- say, how far to the left or right an object appears to one's eyes -- depends on some combination of the values it has in all its dimensions -- say, where it actually is in space. This is hardly radical or surprising.

A matrix then, is a way of representing how things in one frame of reference get transformed into another.

This is all fine and dandy until we start to consider frames of reference that have different ranks -- that is, different numbers of dimensions. To pick the most obvious example, there's the three dimensional world on the one hand, and its appearance in a two dimensional image on the other. Under such a transformation, several different things -- a person's shoulder, a tree in the middle distance, a jagged peak on the horizon many miles away -- can all wind up at pretty much the same 2D location -- the same point in the picture. A whole bunch of information about the full three dimensional structure of the scene is necessarily lost when it's converted into a photo in this way.

At some level, this kind of transformation is fundamentally different from one that preserves all its dimensions. The latter is, at least theoretically, invertible -- all of the original scene information can potentially be recovered -- whereas the former is not. Somewhere along the line information is thrown away, such that we can never get it back.

Matrices representing such operations -- where information is not merely transformed but destroyed -- are termed singular. A characteristic of such matrices is that one or more of their eigenvalues is zero.

Eigen-wha-whosits? Well may you ask.

A matrix represents a transformation that can be applied to any vector data of a suitable rank -- eg, a 3x3 matrix can transform positions in any 3d space -- producing a transformed space of rank no greater -- but quite possibly lower -- than the original. In general, the transformation depends not only on the matrix but also on the data. For example, consider the matrix: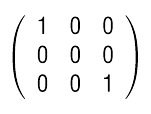

This preserves the x and z dimensions of any data to which it is applied, but any y is brutally truncated to 0. Indubitably, information is tossed away.

Even so, any point -- or vector -- with no y component will slip through entirely unadulterated. Only data in the y direction are lost. Clearly, some information is more liable to be destroyed than other kinds; plenty of information may not be destroyed at all, just perhaps stretched along the way.

We can determine the directions from which data will not deviate under the transform; these are the eigenvectors of the matrix. There are as many of these as the matrix -- which must be square -- has rows or columns. And -- by definition -- every one must be non-zero. Each such vector is associated with an eigenvalue, which is the amount the transformation stretches or shrinks data along that direction. This value can be zero, which was at the root of my confusion today.

A matrix may have one or even more zero eigenvalues, in which case it will be singular. It may not have any zero eigenvectors: even zero eigenvalues must be associated with non-zero eigenvectors.

Because of the way it is formulated, the Q matrix will always have at least one zero eigenvalue. And yet one of the important things we need to do with it -- calculate its exponential -- depends on being able to invert a matrix of its eigenvectors, which in turn requires that that matrix be non-singular. If any eigenvector were zero that would be impossible.

My initial impression was that this would have to be the case, because the Q matrix is singular. No-one present could quite explain why this wasn't so, but fortunately it isn't. Eigenvectors are, by definition, non-zero. When the associated eigenvalues are zero, that just means that there are non-zero vectors that the matrix transforms to zero, and these can be found.

Thus, all remains right with the world. As if you care.
Posted by matt at July 21, 2008 11:00 PM