Case Notes 8

Compact arteriovenous malformations are pathological structures in the vascular system of the brain that can lead to strokes; in contrast to most other kinds of stroke, these usually affect the young. Although the normal brain vasculature is complex, it is also rather orderly, with low order branching and with the arteries and veins only connected via capillaries. An AVM, on the other hand, is tangled, highly branched, and involves direct connection from arteries to veins. As a result, blood pours through the system unpredictably. Potential consequences include hæmorrhage, when the flow breaches the vessel walls; shunt, where the blood flows through the brain area too quickly to properly deliver oxygen and glucose and pick up waste products; and steal, where the increased flow through the AVM diverts blood away from other areas, leading to chronic ischæmia.

Modelling the flow of blood through such a system, and predicting its behaviour, is a tricky business and the methods immature. The governing equations, as so often for fluid dynamics problems, are Navier-Stokes, a complicated partial differential system that can be expressed in a number of ways; here's one:¹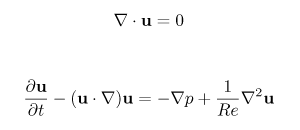

The equations are well characterised and very widely used, in everything from aeroplane design to climate change studies, but they can only be solved analytically in a few very simple cases that do not, on the whole, correspond to realistic problems. They are more commonly estimated numerically, but this doesn't scale well to complex interconnecting topologies such as those found in an AVM.

The system operates on two main length scales: an O(1) scale coming from the vessel shape (the viscous term is significant close to the walls, but the core can be considered inviscid) and an O(Re) scale for the influence of fluid further downstream (for which the core must treated as viscous). In the simplest case -- a long, steady flow through an unbranching vessel of constant cross-section, with no transverse velocity -- there is a pressure gradient from end to end, and the flow has a parabolic profile.²

A soon as you add branching to the picture, even a single 1-2 branch, it significantly complicates the short range effects. To simplify, we assume that the Reynolds number is large (typically ~300 for blood flows in the brain), so that the 1/Re term is small and can be ignored; and that the du/dt term is small as well.³ Thus we need deal only with the steady state.

We can derive a recurrence relation between the pressures and displacements in the mother vessel and the two daughters:

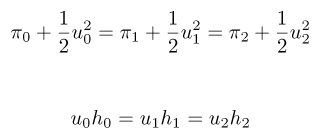which in this simple case can be solved analytically (for the unknown u values). However, as we add more branches, things get rapidly out of hand: the length scales reduce, and the recurrence relations across the generations -- although still "easy" to construct -- become increasingly non-linear, analytically intractable, and in many cases may have multiple solutions.

Numerical simulations can be run of some more complex systems, although again there are fairly low limits to what can be managed with any kind of computational stability. With multi-way branches, unexpected effects can arise; for example, even with a higher pressure upstream of the branching than on each of the downstream branches, situations arise where the flow in some of the daughters goes upstream. With reconnections -- so that the system becomes a network -- things get even worse.

---

1 This version is for an incompressible fluid, and is not the most common formulation. It is non-dimensional and parameterised only by the Reynolds number, Re, which describes the relative importance of viscous and inertial forces. u is a Cartesian distance vector, p is pressure and t is time.
2 That is, the blood flows more quickly in the centre of the vessel and more slowly at the edges, with a (quadratic) smooth change across the width.
3 The justification for the latter assumption escapes me.

Posted by matt at February 14, 2007 10:59 PM