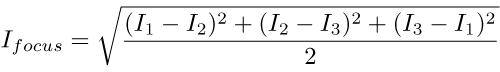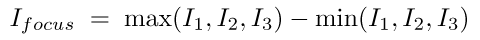Optical Transfer 2

In the previous installment, we used an ideal OTF to simulate the use of structured illumination to eliminate out of focus emissions and get some very crude improvement in lateral resolution. This time out, we're going to make the process work a little better and try it out on a slightly more plausible test image.

The first thing we're going to do is switch from a sine grating to a rectangular pulse pattern. There are several reasons for this. For one thing, a rectangular grating is going to be a lot easier to generate when we start using liquid crystal componentry, which almost always consists of an array of rectangular pixels. For another, it allows for better separation between the bright and dark regions of the focal plane. However, there's a problem.

The sharp edges of a rectangular grating pattern constitute high frequency components, and won't be faithfully transmitted by the OTF. For cases where the grating frequency itself is very low compared to the OTF's cutoff, this effect is more or less negligible -- you're unlikely to notice diffraction blurring between the stripes of a zebra crossing or the squares on a nearby chessboard. But as the bands get narrower and narrower, approaching the diffraction limit, the edges become less and less clear, until the pattern is pretty much equivalent to a sine grating anyway:

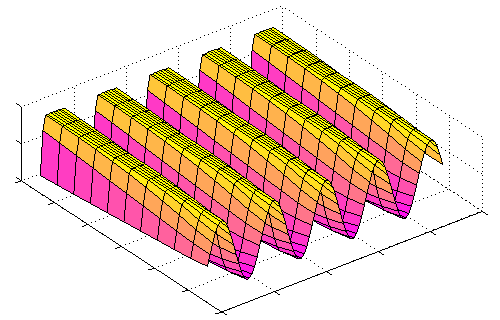
(In this figure, the OTF cutoff frequency is reduced rather than the grating wavelength, to make the effect more visible, but it adds up the same thing.)

Now, as it happens, to get the maximum resolution improvement from our illumination scheme, we want the grating frequency to be fairly close to the cutoff, so even if we're actually using a rectangular pattern, we're never going to get perfect separation. This has some implications for our reconstruction algorithm.

Recall that our primary goal was to separate the constant unfocussed image from the variable focussed one, and to do that we applied this formula:

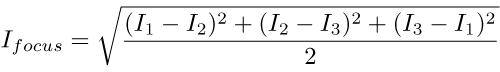
This equation is equivalent to calculating the diameter of a circle that is some distance off the ground, based on the apparent heights of three points equally-spaced around its rim. This works pretty well provided (i) it really is a circle and (ii) the points really are equally spaced. If these assumptions fail -- which is to say, if the pattern is not a perfect sine wave or the three images are not separated by exactly a third of a cycle -- then we start to get banding artefacts.

When the above formula is applied to a square wave, it also gives the correct answer, because it reduces to a somewhat different calculation. In this case, it tells you the distance from the top of the wave to the bottom. We can make this calculation simpler, though, by doing it explicitly, like this:

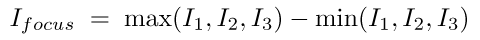
This is actually rather more intuitive in terms of what we want: just the foreground without the background. As a bonus it's also more computationally efficient, robust to uneven phase shifts and very easy to generalise to any number of sample frames.

Needless to say, there's a problem.

Since this formula is subtracting the dark from the light, it depends on there being an adequate separation between those two states. For anything other than a rectangular wave pattern, this will not be the case; and we've already established that our hard-edged rectangular pattern goes all mushy as it passes through the OTF. So not all points in our image will be sampled across the same light range, and there will be some light-dark banding over the image.

There are two things we can do to improve this: we can increase the distance between the light bands in our pattern, and we can increase the number of sample frames we take over a single cycle. For the moment let's gloss over the some of the practical considerations and just assert that we'll use a 2:1 pulse pattern (ie, the dark bands are twice the width of the light), and continue to take just three frames in each direction.

Revisiting our old target pattern with this updated strategy, let's see what we get. Here's a trio of frames taken with the 2:1 grating:

And here are two images generated from vertical and horizontal sets using slightly different applications of the max-min approach:

  

The image on the left takes the max-min over all six frames. This has a tendency to darken the midtones and also to introduce some nasty diagonal artefacts. The one on the right takes the max-min separately for each direction and then adds those results together. This allows for artefacts from one direction to be compensated for in the other. It should also somewhat ameliorate noise problems, which we aren't looking at today but will come back to next time. The differences are not that obvious in these images, but as we'll see below the second approach is actually much more promising.

Out target image so far has been tailored to testing the frequency response, but it doesn't bear much resemblance to any biological sample we'd actually want to look at with fluorescence microscopy. As such, it doesn't necessarily tell us much about how useful our putative techniques might be. It's perfectly possible that some of the improvements we see in the target may be specific to regular patterns of parallel lines and not generalisable to the features found in natural specimens. So, let's introduce a different and hopefully more informative target:

OK, this isn't as neat and pretty as the last one, and is still massively simplified in comparison to an actual cell culture or whatever, but it does include several features of specific relevance to our task:

• The bulk of it is black; the 'fluorescent' parts of it are relatively sparse, as we would typically hope to be the case for tagged biological samples.
• There are different levels of intensity (equivalent to fluorophore concentrations).
• There are different levels of detail: big bits and small bits.
• There are objects inside other objects.
• There are curves. Biological entities are rarely rectilinear.

In addition, you might notice a particular focus on little dots and blobs. The immediate reason for this is that the research areas my work is being done alongside have to do with vesicles -- little packages of chemicals that can be released into the extracellular matrix as needed -- and these will show up as just such blobs. But the same can be said for many other entities in cells that one might want to tag and look at. In general, the ability to distinguish the tiny dots of light in your image is a pretty desirable feature.

OK, so let's take a look at this object through a simulated microscope with a pretty good diffraction limit:

As you can see, we're not losing anything much on the gross structure and even most of the blobs are still distinct. But check out the smudge of smaller grey dots in the upper left; around the larger white blob in the top middle; and in the central disc of the pattern to the lower right. Pretty much lost, right? So what does our new SI technique give?

  

As before, the left is max-min for the full set, right is the verticals and horizontals processed separately and then added. Both formulæ manage to recover more dot detail, and generally sharpen things up a bit. But the diagonal artefacts mentioned before are quite pronounced in the left image -- the verticals and horizontals are overemphasised at the expense of the other directions -- and it isn't as successful at separating the dots.

Let's make the OTF more restrictive and see what happens:

  

  

Note that we've coarsened the illumination pattern in order to get it through the OTF. In the conventional (but clean) upper-left image, we're really starting to lose most of our blobs -- only the biggest can still be clearly distinguished. And the superiority of the two-stage reconstruction is becoming obvious: the exaggerated directions are really starting to confound the lower left image, smearing together blobs that ought to be distinct. By contrast, the grey blobs in the upper right corner and the white ones in the upper left and middle of the lower right hand image are most fairly well separated and countable.

Making things worse still:

  

  

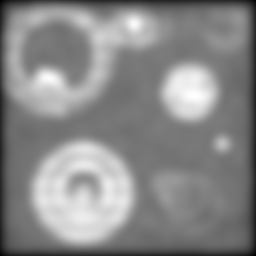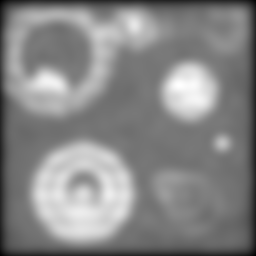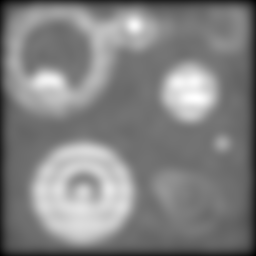
And again:

  

  

By this point, things have gotten pretty ugly. But still, the two-way composite is giving us information that just isn't there in the others. No amount of unsharp mask filtering on the conventional image is going to give us the separation we're still sneaking out via structured illumination.

Which is pretty cool.

But I have an admission to make.

The optical sectioning mechanism is clear enough. And I understand how the SI pattern manages to encode higher levels of lateral detail for transport through the OTF. But I haven't a fucking clue how that detail is being recovered here. At least, not one I can express with any degree of rigour.

All of the analyses of this business that I've seen require some not necessarily complicated but at least deliberate manœuvring to pull out the high frequencies and shift them back to their correct locations in Fourier space. That is not happening in this case. The image recovery is really simple arithmetic. There's no specific deconvolution or phase shifting going on. It's just magic.

Magic is inherently untrustworthy, so at the moment I'm trying, without evident success, to put this on a firmer footing.

In the meantime, I feel reasonably confident that the whole process will get a lot more plausibly-ineffectual when I start taking into account noise and aberrations...
Posted by matt at July 20, 2007 02:36 PM